树链剖分
0.简介
树链剖分是一种基于线段树的优雅的树上点权(边权)和维护算法。使用树链剖分我们可以在O(nlog^{2}n)的优秀时间复杂度内实现对树上一条链上的点权(边权)的查询与修改操作。
需要注意的是,树链剖分对于树形态的变化较难以维护。由于形态变化后必须对树进行重新剖分,才能继续使用线段树对树上信息进行维护。而每次剖分的时间复杂度为O(n),所以对于这种情况我们需要更换换其他算法,如动态树等,本文不涉及。
1.概念
树链剖分引入了几个概念:
重儿子:该父亲所有儿子中子树大小最大的儿子
轻儿子:除重儿子以外的其他儿子
重边:父亲与重儿子之间相连的边
轻边:父亲与轻儿子之间相连的边
重链:由重儿子相连形成的一条链
下图即为一棵剖分完成的树:
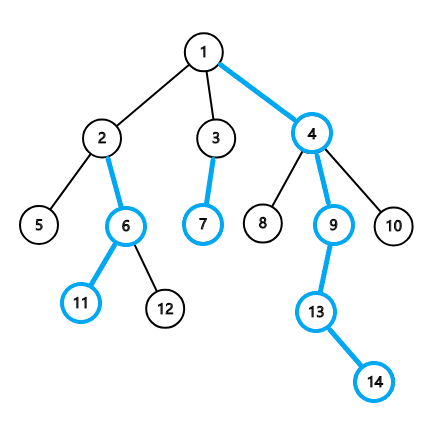
如图所示,所有蓝色的节点均为其父节点的重儿子,所有蓝色的边均为重边,蓝色边连成的链即为重链,下同。
树链剖分则是利用重链,对所有重链上的值使用线段树维护,大大加快查询和的速度。
2.实现
剖分
树链剖分的实现基于两次DFS。
第一次DFS,求出每个节点子树的大小、节点的深度和这个节点的重儿子。
第二次DFS,求出每个节点所在重链顶端节点的编号和DFS序。我们令同一条重链的DFS序是连续的,这样我们就可以使用线段树维护这条链或链上某一段的点权(边权)和。
下面结合代码分析这两次DFS的过程。
代码中出现的变量名及含义:
| 变量名 | 含义 |
|---|---|
| p | 父亲 |
| h | 深度 |
| size | 子树大小 |
| hvy | 重儿子编号 |
| top | 该节点所在重链顶端节点的编号 |
| d | 该节点的DFS序 |
第一次DFS
void dfs(int s) {
for (int i = node[s].f_edge; i; i = e[i].n) {
if (e[i].to == node[s].p) { continue; } //防止访问到父节点
node[e[i].to].p = s; //儿子的父节点即为当前节点
node[e[i].to].h = node[s].h + 1; //儿子的深度为父节点深度加一
dfs(e[i].to); //访问儿子
node[s].size += node[e[i].to].size; //父节点的子树大小为所有儿子节点子树大小之和
if (node[e[i].to].size > node[node[s].hvy].size) { //如果该儿子比原先的重儿子子树大小更大则
node[s].hvy = e[i].to; //该儿子为重儿子
}
}
node[s].size += 1; //子树大小包括当前节点
}
第一次DFS中我们每访问过一个儿子,就将该孩子的size与当前的重儿子的size比较,若该儿子的size比重儿子大,则将重儿子变为该儿子。
在第一次DFS运行完成之后,我们得到以下信息。
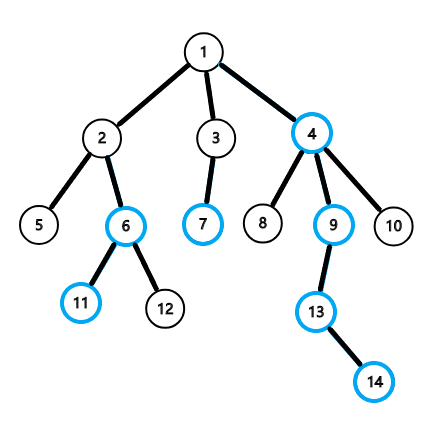
| 编号 | p | h | size | hvy |
|---|---|---|---|---|
| 1 | 0 | 0 | 14 | 4 |
| 2 | 1 | 1 | 5 | 6 |
| 3 | 1 | 1 | 2 | 7 |
| 4 | 1 | 1 | 6 | 9 |
| 5 | 2 | 2 | 1 | 0 |
| 6 | 2 | 2 | 3 | 11 |
| 7 | 3 | 2 | 1 | 0 |
| 8 | 4 | 2 | 1 | 0 |
| 9 | 4 | 2 | 3 | 13 |
| 10 | 4 | 2 | 1 | 0 |
| 11 | 6 | 3 | 1 | 0 |
| 12 | 6 | 3 | 1 | 0 |
| 13 | 9 | 3 | 2 | 14 |
| 14 | 13 | 4 | 1 | 0 |
此时所有节点的重儿子都已被计算出来。第二次DFS中,我们计算出每个节点的DFS序和所在重链顶端的编号(用于求LCA时加速)。
void subdiv(int s, int h) { //h为当前重链顶端
node[s].top = h; //将当前节点所在的重链顶端编号赋值为h
node[s].d = cnt++; //赋值DFS序
sg.insert(1, node[s].d, node[s].d, node[s].v); //将当前节点点权加入线段树维护
if (!node[s].hvy) { return; } //无重儿子则是叶节点,无需执行下面访问节点的操作
subdiv(node[s].hvy, h); //先访问重儿子,保证DFS序连续
for (int i = node[s].f_edge; i; i = e[i].n) {
if (e[i].to == node[s].p || e[i].to == node[s].hvy) { continue; } //防止访问父节点和重儿子
subdiv(e[i].to, e[i].to); //轻儿子所在的重链顶端节点一定是他本身
}
}
第二次DFS后我们得出每个节点所在的重链顶端节点的编号和DFS序,并将每个节点的信息加入线段树维护。

| 编号 | top | d |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 8 |
| 3 | 3 | 13 |
| 4 | 1 | 2 |
| 5 | 5 | 12 |
| 6 | 2 | 9 |
| 7 | 3 | 14 |
| 8 | 8 | 6 |
| 9 | 1 | 3 |
| 10 | 10 | 7 |
| 11 | 2 | 10 |
| 12 | 12 | 11 |
| 13 | 1 | 4 |
| 14 | 1 | 5 |
(注意,DFS序因建边顺序不同可能有变化,上表只是一种可能的DFS序)
至此,我们完成了树链剖分的重要部分——剖分。经过两次DFS,我们将树剖分成了多条链,并使用线段树维护每条链上的信息。
查询
根据DFS序的连续性,同一棵子树上的DFS序是连续的,我们可以很轻松的写出查询某节点子树的点权和的操作:
int sum(int n) {
return sg.query(1, node[n].d, node[n].d + node[n].size - 1) % mod;
}
是的,极其简单的一行线段树查询操作,这就是DFS序带来的便利。
那么如何查询两点之间的全部点权之和呢?我们继续结合代码分析:
int sum(int x, int y) {
int fx = node[x].top, fy = node[y].top, ans = 0;
while (fx != fy) { //当两节点不在同一条重链上时
if (node[fx].h >= node[fy].h) { //从深度大的一边开始往上跳
ans = ans + sg.query(1, node[fx].d, node[x].d); //加上这一条重链上的点权和
x = node[fx].p; //向上跳一次
fx = node[x].top;
} else { //同上
ans = ans + sg.query(1, node[fy].d, node[y].d);
y = node[fy].p;
fy = node[y].top;
}
}
if (node[x].d <= node[y].d) { //两点跳到同一条重链上后
ans = ans + sg.query(1, node[x].d, node[y].d); //加上这两点之间的点权和
} else {
ans = ans + sg.query(1, node[y].d, node[x].d);
}
return ans;
}
我们利用DFS序的连续性,在O(logn)的时间复杂度内求出一条链上的点权和,大大加快了统计两点之间点权和的速度。
修改
修改和查询同理,将线段树查询改为修改即可,这部分就交给各位自己完成=v
3.时间复杂度
树链剖分的两个性质:
1. 如果(u, v)是一条轻边,那么size(v) < size(u)/2;
2. 从根结点到任意结点的路所经过的轻重链的个数必定都小于logn.
可以证明,树链剖分的时间复杂度为O(nlog^2n)
4.代码
以下代码以Luogu P3384为例