Day 3

教练果然是个守信的人呐
被昨天的满屏省选数学题虐得体无完肤后，Day 3迎来了较为舒适的“提高”难度题目。稍微瞟一眼QwQ

T1 A

是的今天题目标题就是这么神奇
这个题面似乎有点问题？首先m和b是没有下界的，题面并没有说明m,b为正整数。其次，题目并没有说明矩形的放置方式。例如对于样例所给的情况，下图的放置方法也是可行的，并且比样例所给出的答案更优。

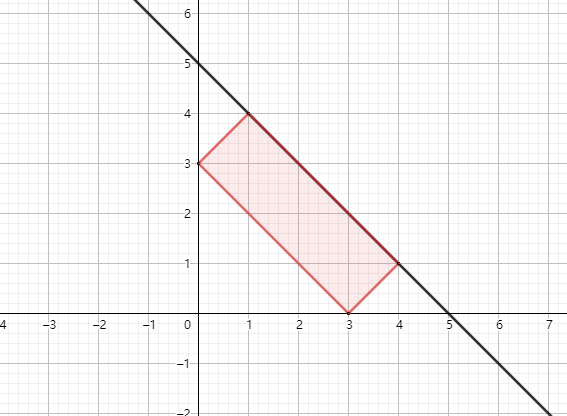
从样例中可以推测出矩形只可与坐标轴平行放置。考虑到包含每个点的贡献始终是正的，我们使包含点的个数越多越好。显然，矩形其中一个顶点为原点，一个顶点在直线上，其余两个点可通过在直线上的点确定。可以推出对于每个点(x,y)
sum=(x+1)* \frac{y^{2}+y}{2}+(y+1)* \frac{x^{2}+x}{2}
注意到数据范围十分友好，直接枚举直线上每个整点即可。

T2 B

毒瘤线段树。
题解的表述：明显到爆的线段树 这哪里明显了
考场上的思路是类似于软件包管理器那题的区间赋值线段树再枚举左端点，但这个数据范围注定了跑不过大部分点，于是咱加了个二分试图优化，结果居然成了负优化？？QwQ
然后czh dalao就AC了QwQczh怎么能这么强啊啊啊啊啊Qw
然后就在czh dalao的指导下调了一个下午的这题，顺便把日记鸽到了今天==
正解的思路似乎类似于染色的维护最左侧、最右侧再判断是否跨区间及是否合并的思路。我们维护每个区间最左端连续的0的数量lz，最右端连续的0的数量rz，及区间内最长连续0的长度len。我们在更新时分别处理这三个值

i) lz

(待补图)
由上图可以看出，每次更新时父节点的lz与左孩子的lz有关。若左孩子lz没有占满整个区间，则显然父节点的lz与左孩子相同，否则我们观察得出父节点的lz为左孩子与右孩子的lz之和.

ii) rz

rz的处理方法与lz类似，类比一下应该很容易写出来。

iii) len

(待补图)
区间内最长连续零只有可能有三种情况：全部在左区间、跨过左右区间、全部在右区间。我们令len=min{l.len,l.rz+r.lz,r.len}即可。

有了维护的这些值，接下来我们看一下该如何求解。
首先，我们知道对于所有可行的方案，我们选择尽可能靠左侧的方案。则
1.若左侧已有连续的足够长的零，则直接返回左端点即可。
2.否则我们尽可能选择靠左的端点，若lc.len>=len，则进入左子树递归处理。
3.否则我们考虑跨区间的零。若lc.rz+rc.lz>=len，则我们返回lc.r-rz+1,即此跨区间连续零的左端点位置。
4.否则考虑右子树。由于我们要求的是最靠左的连续零的左端点位置，我们应优先考虑位于区间中间的连续零。即若rc.len>len，则进入右子树递归处理。
5.否则考虑右侧最靠右的一段连续零，即若rc.rz>len，则返回rc.r-rc.rz+1。
6.若以上全部不成立，则意味着无解，返回-1即可。

至此，这道毒瘤题就被我们搞定了。至于实现嘛。。。祝您好运咯=w

T3 C

题面描述是求对于每个子串的最短的循环节。小蒟蒻并不会这道题QwQ考场上打的暴力毫无疑问地T了满屏。
么这题该怎么搞定呢?考虑到我们要求循环节，即重复的相同的子串。要找相同的子串有什么比较好的做法呢？KMP!KMP算法中next[i]的意义为字符串长度为i的前缀中相同的前缀后缀长度。关于KMP算法，请左转百度。
因此，我们可以利用next数组的这个性质进行计算。若i|i-next[i]，则这是一个循环的子串，循环次数为i/(i-next[i])。